
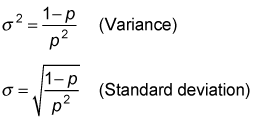
Let two independent random variables $X_1$ and $X_2$ have same geometric distribution.
#METHOD OF MOMENTS GEOMETRIC DISTRIBUTION SERIES#
Many of the basic power series studied in calculus are hypergeometric series, including the ordinary geometric series and the exponential series. Then the random variable $X$ take the values $x=0,1,2,\ldots$.įor getting $x$ failures before first success we required $(x+1)$ Bernoulli trials with outcomes $FF\cdots (x \text\\ A (generalized) hypergeometric series is a power series k 0akxk where k ak + 1 /ak is a rational function (that is, a ratio of polynomials). Y1 Further, Stats, Distributions, Discrete Uniform Distribution. Let random variable $X$ denote the number of failures before first success. Y1 Further, Stats, Distributions, Geometric Distribution, Geometric Distribution MS. Geometric DistributionĬonsider a series of mutually independent Bernoulli’s trials with constant probability of success $p$ and probability of failure $q =1-p$. In this tutorial we will discuss about various properties of geometric distribution along with their theoretical proofs. The choice of the definition is a matter of the context.

Write down the likelihood as a function of the observed dataX1. There are two different definitions of geometric distributions one based on number of failures before first success and other based on number of trials (attempts) to get first success. A geometric distribution is thedistribution of the number of coin ips needed to see one head. Geometric distribution is used to model the situation where we are interested in finding the probability of number failures before first success or number of trials (attempts) to get first success in a repeated mutually independent Beronulli’s trials, each with probability of success $p$.


 0 kommentar(er)
0 kommentar(er)
